Ángulos y Arcos: Que son, medición y ejemplos

El cálculo trigonométrico es esencial en toda ciencia en donde hallan relaciones entre ángulos y magnitudes. Es por ello que en este artículo abordaremos los diferentes sistemas de medición de ángulos y como estás medidas se relacionan con el arco y el radio de manera directa.

Es importante mencionar que en la resolución y análisis de los elementos triangulares, la trigonometría frecuentemente hace uso de la geometría y el álgebra, pero sin confundirse con ninguna de estas dos ciencias matemáticas.

¿Qué es un ángulo en geometría?

Ángulo en la palabra puramente latina (angulus) qué significa esquina o rincón. En geometría se llama ángulo la abertura entre dos rectas que parten de un mismo punto.

Consideremos un segmento de recta relacionado con un sistema de ejes cartesianos, Figura 1. Supongamos que la recta OP inicialmente ocupaba la posición O-X y que ha girado alrededor del punto O manteniéndose en un mismo plano, entonces decimos que la recta ha engendrado un ángulo. Dicho ángulo lo podemos designar con una letra minúscula del alfabeto griego, θ por ejemplo, o por medio de las letras latinas escribiendo: ángulo XOP.

Por convención universal se consideran ángulos positivos los engendrados por una recta que gira en sentido contrario a las manecillas del reloj; y como ángulos negativos cuando las rectas generatrices giran en el mismo sentido de las manecillas del reloj.

El segmento O-P1 que se considera como origen del ángulo se llama lado inicial y el segmento de recta OP lado terminal.

Te puede interesar: Los 7 Tipos de Triángulo: Clasificación, Conceptos y Ejemplos

Medidas de Ángulos y Arcos

Medir una cantidad es compararla con otra que se toma como unidad. Los ángulos como los arcos son mesurables, y por tanto medir un ángulo es compararlo con el ángulo unidad. Lo mismo que medir un arco de circunferencia es compararlo con otro arco de la misma circunferencia, o de otra con igual radio, que se ha tomado como unidad.

Entre los varios sistemas de medida de ángulos y arcos los tres principales son: el sexagesimal, el centesimal, y el circular o radial. A continuación se abordarán cada uno de los sistemas y su composición.

Sistema Sexagesimal

En este sistema se considera la circunferencia dividida en 360 partes iguales, Cada una de estas partes se llama grado. Un grado es pues la trescientos sentaava parte de la circunferencia.

El grado se subdivide en 60 partes iguales llamadas minutos; y el minuto a su vez se subdivide en 60 partes iguales que reciben el nombre de segundos.

Estas divisiones de sesenta en sesenta justifican el nombre de sexagesimal que se da al sistema.

Sistema Centesimal

Se llama así porque sus divisiones van de 100 en 100. Se considera la circunferencia dividida en 400 partes iguales. Un grado en sistema centesimal vale pues un cuatrocientosavo de circunferencia.

El grado se subdivide en 100 minutos y el minuto a su vez en 100 segundos. Este sistema es usado principalmente en geodesia.

Sistema Circular

Este sistema se llama también natural  y toma como unidad de medida el arco de circunferencia que tiene como longitud el radio de dicha circunferencial. Al arco unidad se da el nombre de radián.  Sabemos que la circunferencia vale 2πr; si dividimos por r tenemos por tanto que la circunferencia mide 2π radianes.

Relaciones entre Radián, Grado Sexagesimal  y Grado Centesimal

Llamando con la letra c la circunferencia podemos escribir:

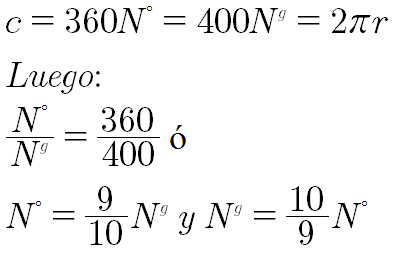
Entre grado sexagesimales y radianes tenemos la siguiente relación:

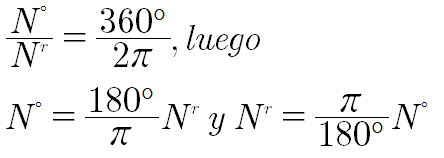
Ejemplo 1. ¿Cuántos grados centesimales hay en 90 grados sexagesimales?

Ejemplo 2. En sistema centesimal ¿Cuánto vale el ángulo 30° 15' 40'' ?

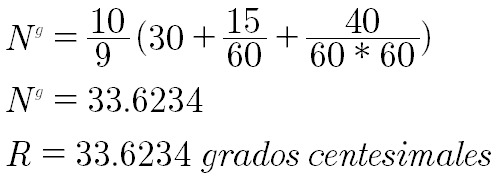
Ejemplo 3. ¿A cuántos grados sexagesimales equivales un radián?

Ejemplo 4. ¿Cuántos radianes vale un grado sexagesimal?

Relaciones entre Radio, Ángulo y Arco

La relación que se establece entre el radio (R), el ángulo(θ) en radianes y el arco o longitud de arco (S) es la siguiente:

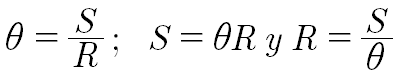
Ejemplo. ¿Qué espacio recorre un barco al girar un ángulo de 30° sobre una circunferencia de 50 metros de radio?

¿Qué es el sector circular?

El último concepto a tratar en este artículo es el sector circular, el cual es el segmento de círculo limitado por dos radios y el arco subtendido. En la siguiente figura tenemos por tanto dos sectores circulares, uno limitado por el arco AMB y otro limitado por el arco ANB.

Tal como evidenciamos en la figura, el arco del sector circular es igual al semiproducto del arco por el radio. Pero gracias a que sabemos que la longitud se relaciona con el ángulo barrido, al final podemos hacer uso de dos fórmulas.